
Les Maths avec Léonie - CM1
Un outil progressif, complet et innovant
« À chaque étape de la conception de cette méthode, nous avons vraiment eu à cœur de penser un outil pédagogique à la fois progressif, complet et innovant, qui vous permette de préparer et animer des séances vivantes et efficaces pour tous vos élèves.
Nous espérons que la méthode Les Maths avec Léonie répondra au mieux à vos attentes et accompagnera vos élèves dans le plaisir de faire des mathématiques.»
Les auteures

Les auteures
Josiane Hélayel
Coordination d'ouvrage et auteure
Professeur-formateur à l'IUFM d'Antony et autrice de nombreux ouvrages : Collections « Place aux maths » et « Au rythme des maths » (Bordas) ; Collection « 100 idées » (Éditions Tom Pouce) ; Situations-jeux pour les apprentissages en mathématiques (Retz)
Yves Doher
Auteur
Magali Haddad Tsakalos
Auteure
PEMF - Ecole élémentaire Velpeau/CM1 - Antony
Après une licence pluridisciplinaire scientifique et sciences de la matière à l’université d’Orsay Paris Saclay, Magali a obtenu le concours de professeur des écoles en 2003. Depuis elle a pu enseigner dans tous les niveaux de l’école élémentaire. Elle a notamment travaillé 10 années en REP+, dans les communes de Villeneuve-la- Garenne puis de Bagneux. Depuis 2014, elle exerce à Antony, en cycle 3 principalement.
En 2013, l’obtention du CAFI-PEMF lui permet de contribuer à la formation initiale auprès des étudiants en master MEEF et à la formation continue au sein de sa circonscription, en proposant notamment des actions de formation en mathématiques.
Dans sa pratique professionnelle, Magali s’attache à ce que les situations et les outils pédagogiques proposés rendent ses élèves acteurs de leurs apprentissages et contribuent aux progrès et au développement de tous. C’est ainsi que Magali a accueilli avec enthousiasme le projet de travailler sur la méthode « Les maths avec Léonie » puisque les axes de travail proposés concordent avec sa vision de l’enseignement. En effet, on y rencontre des séances dont les fondements reposent sur un maximum de manipulations et d'interactions entre les élèves mais aussi sur une progressivité des apprentissages. L’enseignement des mathématiques y est explicite et place les élèves au cœur des apprentissages, ce qui permet de construire les notions en y mettant du sens. Enfin la coopération entre les élèves, qui sont amenés régulièrement à travailler en groupe lui tient particulièrement à cœur. Les élèves sont ainsi encouragés à s'entraider, se confronter, se positionner, à écouter, ceci favorisant la bienveillance entre pairs et l'implication des élèves qui sont amenés à penser par eux-mêmes.
Anne Guinchard
Auteure
Professeur des écoles à l'école Edmond Blanguernon d'Antony en CM2
Après un bac scientifique spécialité maths, Anne Guinchard a obtenu une maitrise de STAPS de l’Université Joseph Fourier de Grenoble. Elle a alors obtenu le CAPE et a entamé sa carrière de professeur des écoles en 2006 en tant que BDRS dans tout le département des Hauts de Seine où elle a travaillé dans plus d’une quarantaine d’écoles (dans 24 des 27 communes du département !), accumulant ainsi une expérience variée et riche. Elle a alors été affectée en maternelle à Fontenay-aux-Roses puis à Villeneuve-la-Garenne. Elle a ensuite rejoint la commune d’Antony en tant que ZIL où elle a enseigné dans tous les niveaux de classe, de la toute petite section au CM2. Depuis 2019, elle enseigne en CM2 à Antony et s’intéresse particulièrement à la recherche et la mise en place de nouvelles approches pédagogiques. Soucieuse de contribuer à la formation, elle assume également la fonction de Maitre d’Accueil Temporaire.
Les choix didactiques
Une progression réfléchie
Comme dans la méthode originale de Singapour, les notions abordées sont regroupées par blocs de façon à passer plusieurs séances d’affilée sur une même notion afin de mieux ancrer les apprentissages. Tous les domaines du programme sont ainsi abordés dans chaque période de l’année et les Repères de progression annuels officiels sont respectés. La progression en calcul mental est construite parallèlement à celle du domaine « Nombres et calculs » pour permettre aux élèves de s’entraîner au quotidien, conformément aux programmes. Ces activités fournissent l’occasion de réinvestir et de consolider les notions rencontrées dans les leçons ou dans les niveaux précédents. Elles permettent parfois de préparer ou d’introduire la notion qui va être abordée dans la séance du jour.
Des choix nourris dans chaque domaine
Cette adaptation s’appuie sur une réflexion didactique fondée sur des observations en classe et les résultats de travaux de recherche récents. Tous les contenus proposés sont conformes aux Programmes de CM1 (B.O. du 30 juillet 2020) et aux Repères annuels de progression et attendus de fin d’année 2019. Ils s’appuient également sur des documents d’accompagnement, notamment « Fractions et décimaux au cycle 3 », « Proportionnalité au cycle 3 » et « Calcul en ligne au cycle 3 » et tiennent compte au mieux des pratiques et des besoins des enseignants sur le terrain.
Nombres et calculs
✓ En numération, en s’appuyant sur les acquis du CE2,
l’apprentissage de la numération écrite précédant l’apprentissage de
la numération orale se poursuit. Après avoir travaillé spécifiquement
l’aspect décimal et l’aspect positionnel de notre système de
numération, ces notions sont réinvesties conjointement alors que le
champ numérique s’agrandit.
Par les manipulations proposées au début de chaque leçon, l’élève
prend conscience que les nombres entiers ne suffisent pas pour
résoudre toutes les situations mathématiques. La construction des
fractions et des nombres décimaux va s’appuyer sur ce constat.
Différents contextes (partage de grandeurs, expression de longueurs,
repérages sur droites graduées) vont permettre d’installer du sens sur
la notion de fraction. C’est par les fractions décimales que l’élève sera
amené à appréhender la notion de nombre décimal.
Ces étapes assurent une progressivité adaptée à tout profil de classe.
✓ En calcul, l’accent est mis d’une part sur un entraînement quotidien de calcul mental proposé dans le Guide pédagogique, et d’autre part sur le calcul en ligne pour utiliser les propriétés de chaque opération avant l’introduction des opérations posées.
✓ La résolution de problèmes, présente dans chaque période dès le début d’année, contribue à assurer la construction du sens des opérations. Les différentes typologies de problèmes additifs et multiplicatifs sont abordées à l’aide de schémas en barres qui permettent d’apprendre à organiser et aident à structurer sa recherche. Dans les leçons abordant la notion de proportionnalité, les élèves mettent en oeuvre des procédures personnelles puis sont progressivement amenés à structurer ces procédures en appui sur les rapports entre les nombres et les propriétés de linéarité.
Espace et géométrie
✓ En géométrie, la progression spiralée permet d’appréhender les premières propriétés de figures géométriques. Le vocabulaire, précis et adapté, est mis en place au cours de manipulations et de situations d’actions et prend sens pour les élèves. Il leur permet de passer progressivement d’une géométrie perceptive, dans la continuité du cycle 2, à une géométrie instrumentalisée.
Grandeurs et mesures
✓ Des grandeurs différentes sont abordées à chaque période. Les nouvelles notions de CM1 sont travaillées de manière progressive, en commençant par une estimation visuelle ou un report de longueurs avec du matériel de manipulation avant de démarrer le travail sur les unités de mesure.
Les auteurs
L'organisation de la méthode au CM1
La méthode de Singapour adaptée pour les écoles françaises
Les Maths avec Léonie est une collection complète de manuels scolaires reprenant les contenus originaux et la méthode pédagogique mis en place à Singapour par le Ministère de l’éducation.
Les directives du gouvernement singapourien ont été mises en forme dans des manuels scolaires par différents éditeurs, notamment par Marshall Cavendish Education, dont la collection My Pals are Here! a ensuite fait ses preuves dans de nombreux pays.
Les Maths avec Léonie reprend les contenus de My Pals are Here!. Ces contenus ont été adaptés par des enseignants français à l’organisation de l’école primaire française, aux élèves et aux pratiques des enseignants.
Les Maths avec Léonie CM1 est donc conforme aux programmes du CM1 (B.O. du 30 juillet 202), aux Repères de progression et aux attendus de fin d’année 2019, ainsi qu’au Socle commun de connaissances, de compétences et de culture.
Manipuler, observer, apprendre
Les Maths avec Léonie CM1 reprend dans sa structure les six temps d’apprentissage de la pédagogie de la méthode de Singapour :
- manipulation,
- observation,
- modélisation mathématique,
- entraînement-répétition,
- utilisation de jeux mathématiques,
- résolution de problèmes.
On retrouve ces six étapes dans les rubriques des Cahiers.

Les trois premières étapes sont abordées lors de la mise en place de la notion étudiée
Les autres sont travaillées à travers les rubriques qui correspondent à l’entraînement des élèves

Mise en place de la notion étudiée
L’approche :
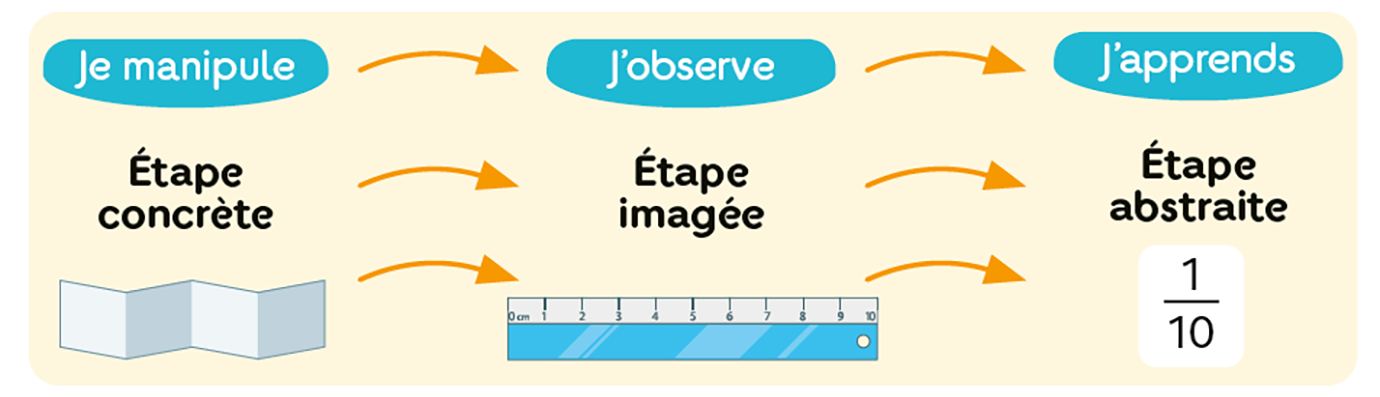
Étape concrète (manipulation) => Étape imagée (observation) => Étape abstraite (modélisation mathématique)
donne du sens à chaque notion mathématique étudiée en passant progressivement
du concret à l’abstrait. Elle permet aux élèves de comprendre la notion étudiée avant d’en apprendre
sa mise en forme mathématique (vocabulaire, notations, règles, etc.).

L'entraînement des élèves
Les élèves s’entraînent dans la rubrique À mon tour. Les exercices qui leur sont proposés sont guidés et appliquent la notion étudiée. Ils sont de formes différentes et de difficulté croissante. La répétition d’exercices similaires permet d’ancrer les connaissances.
- Cette rubrique propose dans chaque leçon :
- des exercices d’application,
- des jeux,
- des problèmes,
- des prolongements ludiques.

Des exercices supplémentaires sont proposés sur le site Ressources dans les Fiches d’entraînement en autonomie. Ces fiches sont téléchargeables gratuitement. Elles offrent aux élèves un temps de travail en autonomie sur des exercices similaires à ceux qui auront été effectués en classe entière sur les Cahiers.
Une progression spiralaire
Dans la méthode de Singapour, les élèves étudient la même notion durant plusieurs séances d’affilée. En
restant ainsi sur la même notion mathématique, les élèves l’assimilent à leur rythme : certains dès la première
séance, d’autres de manière plus progressive.
Le fait d’enchaîner plusieurs séances sur la même notion est un des piliers fondateurs de la méthode de
Singapour. Ce principe a été repris dans Les Maths avec Léonie.
Chaque notion déjà étudiée est réinvestie dans de nouvelles leçons tout au long de l’année, puis dans
les niveaux supérieurs. Lors de l’introduction d’une nouvelle notion, l’élève doit utiliser des compétences
mathématiques déjà étudiées et maîtrisées. La résolution des exercices lui permet de réinvestir ses connaissances
à bon escient, à des niveaux de difficulté parfois supérieurs. De même, le calcul mental proposé au
début de chaque séance est l’occasion de travailler systématiquement les notions des leçons précédentes.
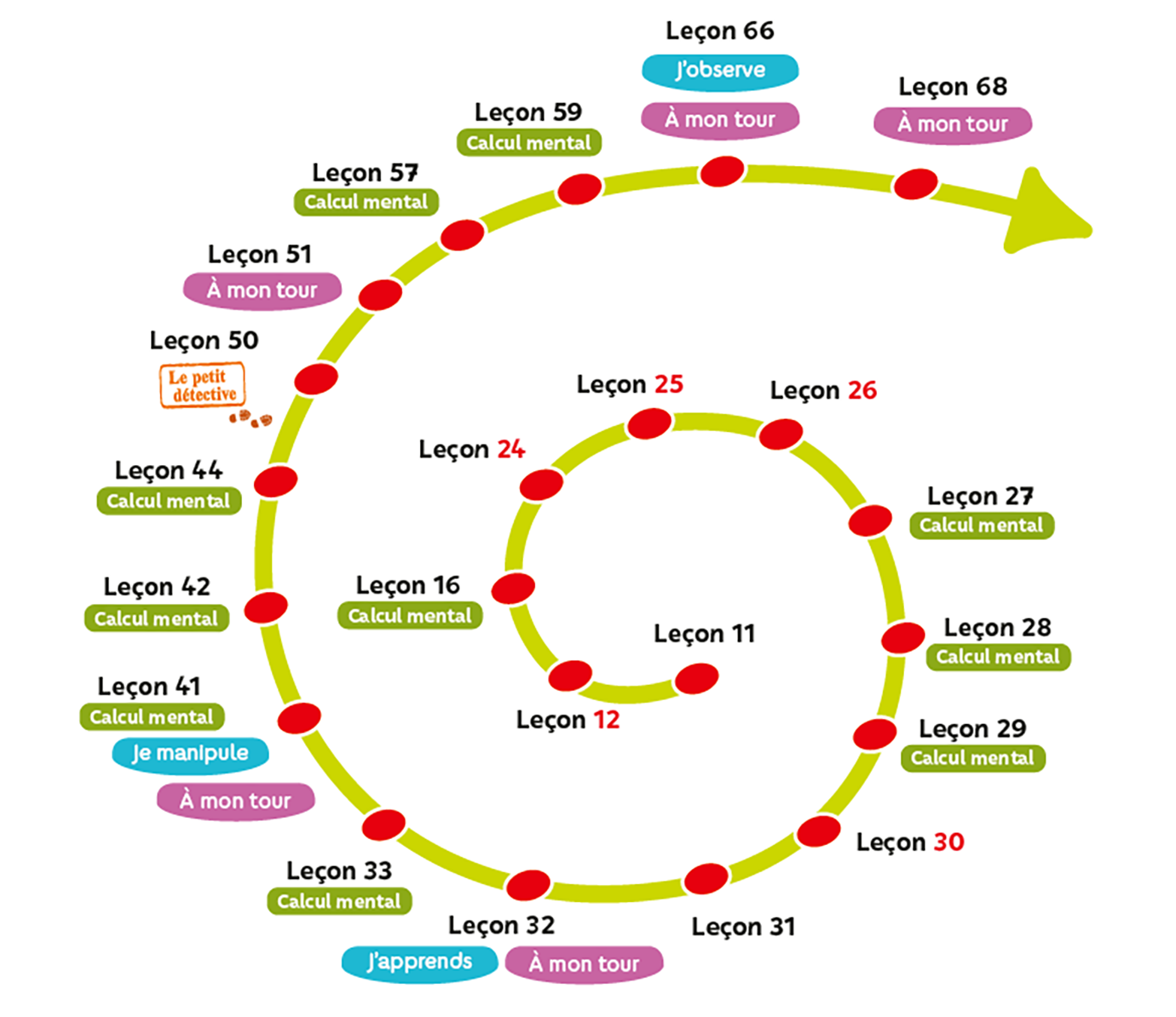
Ainsi la leçon 11, qui introduit pour la première fois les fractions, est réinvestie et approfondie de nom breuses fois jusqu’à la fin de l’année dans les leçons suivantes :
- Leçon 12 : Découverte des fractions simples (2), Cahier 1 p. 40, toutes les activités de la leçon
- Leçon 16 : Nombres jusqu’à 999 999 (1), Cahier 1 p. 54, Calcul mental
- Leçon 24 : Fractions simples, Cahier 1 p. 74, toutes les activités de la leçon
- Leçon 25 : Découvertes des fractions décimales, Cahier 1 p. 76, toutes les activités de la leçon
- Leçon 26 : Fractions décimales (1), Cahier 1 p. 80, toutes les activités de la leçon
- Leçon 27 : Droites parallèles, Cahier 1 p. 82, Calcul mental Leçon 28 : Problèmes de proportionnalité (1), Cahier 1 p. 86, Calcul mental
- Leçon 29 : Problèmes additifs et multiplicatifs à plusieurs étapes, Cahier 1 p. 88, Calcul mental
- Leçon 30 : Fractions décimales (2), Cahier 2 p. 6, toutes les activités de la leçon
- Leçon 31 : Découverte des nombres décimaux, Cahier 2 p. 10, toutes les activités de la leçon
- Leçon 32 : Nombres décimaux (1), Cahier 2 p. 14, J’apprends À mon tour
- Leçon 33 : Quadrilatères et quadrilatères particuliers, Cahier 2 p. 16, Calcul mental
- Leçon 41 : Nombres décimaux (2), Cahier 2 p. 42, Calcul mental, Je manipule, À mon tour
- Leçon 42 : Nombres décimaux (3), Cahier 2 p. 44, Calcul mental
- Leçon 44 : Figures complexes : vers les programmes de construction, Cahier 2 p. 50, Calcul mental
- Leçon 50 : Durées, Cahier 2 p. 64, Le Petit Détective
- Leçon 51 : Problèmes sur les grandeurs (1), Cahier 2 p. 66, À mon tour
- Leçon 57 : Nombres jusqu’à 999 999 999 (3), Cahier 2 p. 82, Calcul mental
- Leçon 59 : Aires, Cahier 2 p. 86, Calcul mental
- Leçon 66 : Volumes et contenances, Cahier 2 p. 102, J’observe À mon tour
- Leçon 68 : Problèmes sur les grandeurs (2), Cahier 2 p. 108, À mon tour
Le Guide pédagogique : un véritable outil d'accompagnement
Pour accompagner l’enseignant dans la mise en œuvre de la méthode, le Guide pédagogique de la méthode
Les Maths avec Léonie, très complet, propose des conseils de gestion de classe pour chaque activité.
Sous le titre de chaque leçon sont rappelés le domaine concerné (Nombres et calculs, Grandeurs
et mesures ou Espace et géométrie) et les compétences du programme traitées dans
la leçon.
La structure et le déroulé des commentaires
Contexte général : les programmes
Chaque chapitre de ce Guide pédagogique correspond à une leçon des Cahiers. Il débute par la contextualisation de la leçon au sein des programmes en vigueur, et s'appuie sur les Repères de progression et les attendus de fin de CM1.
Commentaires des auteurs
Pour chaque leçon, les auteurs expliquent leurs choix et leurs intentions pédagogiques. Ils partagent leur analyse des contenus des programmes et de leur progression, tout en faisant le lien avec la méthode de Singapour.
Les auteurs précisent les notions mathématiques mises en jeu et exposent les éventuelles difficultés qu’elles peuvent induire, ou les cas particuliers qu’elles peuvent contenir.
Calcul mental
Une activité qutotidienne de calcul mental est proposée. Ces activités de calcul mental peuvent être réalisées à différents moments de la journée : le matin ou en début d'après-midi, comme rituel, ou juste avant la séance de mathématiques.
Il faut compter environ 15 minutes pour réaliser une activité de calcul mental.
Le professeur dispose du déroulement de chaque séance de calcul mental : compétence travaillée, conseils, mise en place, questions et corrections.

Déroulement des séances
En tout, dans une année scolaire, il y a 36 semaines d’école, soit 144 jours. Dans l’emploi du temps d’une classe de CM1, il faut prévoir en moyenne 1 h 15 min de mathématiques par jour, le calcul mental occupant environ 15 minutes sur cet horaire.
Ces quinze minutes peuvent être proposées à différents moments de la journée : en
arrivant le matin, en début d’après-midi ou juste avant une séance de
mathématiques. Il reste donc environ 144 heures à partager entre les leçons et les
évaluations. Ce fichier est découpé en 68 leçons : 47 leçons de 2 pages et 21 leçons
de 4 pages. Chaque leçon nécessitera entre 2 et 4 séances (parfois une seule
séance pour certaines leçons courtes ou de révision) :
• Chaque séance démarrant une leçon contiendra une manipulation suivie d’une
institutionnalisation et d’un exercice d’application immédiate (1 heure en tout
qui peut être découpée dans la journée).
• La séance suivante contiendra une série d’exercices, un jeu, un problème à faire
en collaboration et/ou un problème de recherche (entre 30 minutes et 45
minutes) ; puis environ 15 minutes de remédiation ou d’approfondissement
pourront être proposés à un autre moment de la journée (1 heure en tout).
Les Cahiers de l’élève, le Fichier de différenciation et les Fiches d’entraînement en autonomie téléchargeables sur le site Ressources permettent à l’enseignant de proposer un travail adapté à chaque élève. L’objectif n’est pas que tous les élèves finissent tous les exercices, mais que tous puissent valider la compétence étudiée.
Après un travail sur le Cahier en classe entière, l’enseignant pourra organiser des ateliers ou des groupes de besoin. Il pourra laisser aisément certains élèves travailler en autonomie sur la Fiche d’entraînement en autonomie de la leçon car les exercices qui y sont proposés sont très semblables à ceux du Cahier. Cela lui permettra de se rendre disponible pour travailler avec d’autres élèves sur des exercices de remédiation du Fichier de différenciation, par exemple, ou sur le Jeu de la leçon.
Activités Observer – Manipuler – Apprendre
L’approche Je manipule => J’observe => J’apprends, fondée sur les trois étapes concrète – imagée – abstraite est mise en scène dans les trois premières rubriques de chaque leçon pour que les élèves puissent donner du sens à la notion mathématique étudiée en passant progressivement du concret à l’abstrait. Dans cette approche, les élèves sont amenés à comprendre la notion étudiée avant d’en apprendre sa mise en forme mathématique (vocabulaire, notations, règles, etc.). Les précisions didactiques fournies dans les commentaires du Guide pédagogique aideront l’enseignant à articuler ces trois temps avec sa classe.
Je manipule
Les commentaires de ce Guide pédagogique détaillent la mise en place (groupes, durée, conseils) de cette activité et donnent sa correction.
Des prolongements possibles sont également proposés, notamment pour pouvoir faire le lien avec les autres activités.
J’observe
Cette partie est une introduction au cours. Sa mise en place (durée, conseils) et sa correction sont précisées dans le déroulé de chaque leçon.
L’élève doit ici compléter une activité qui découle de la manipulation précédente. Il est donc important de laisser le temps aux élèves de compléter les éléments sur leur Cahier et de vérifier que toutes les réponses notées sont justes. L’enseignant choisira de corriger les erreurs (s’il y en a peu) ou donner la réponse attendue au tableau (s’il y a trop d’erreurs).
J’apprends
Cette partie représente le cours. C’est l’occasion de reprendre autrement les résultats des deux activités précédentes. Des conseils sont donnés dans cette optique.
L’élève n’a donc pas à la compléter. Le professeur pourra lire cette partie avec les élèves ou réécrire certaines notions au tableau ou encore utiliser des affiches téléchargeables sur le site Ressources.
À mon tour
Ici, commence le travail d’entraînement des élèves. Les corrections, les erreurs possibles attendues et les conseils de remédiation sont précisés pour chaque exercice afin de prendre en compte le rythme de chacun.
Les corrections des exercices sont également présentes dans les cahiers numériques pour l'enseignant afin de pouvoir les vidéoprojeter pour une correction collective.
Jeu
Cette partie contient un renvoi vers un jeu mathématique expliqué dans le Livret de jeux. Le matériel nécessaire et le déroulement du jeu sont expliqués dans le Guide pédagogique. Les élèves abordent le jeu au fur et à mesure qu’ils finissent les exercices précédents. Laisser se former les groupes, ou imposer des règles (du type un garçon et une fille, deux élèves côte à côte, un élève en difficulté avec son tuteur, etc.).
Distribuer un Livret de jeux à chaque groupe et expliquer la règle du jeu à l’aide des illustrations. Les élèves pourront se référer à ce livret pour se remémorer la règle. Pour expliquer concrètement le déroulement du jeu, l’enseignant peut inviter un élève à venir jouer avec lui au tableau en montrant les actions à réaliser à la classe. Tous les élèves doivent avoir expérimenté le jeu. Ceux qui n’ont pas pu le faire lors de la séance pourront y jouer la séance suivante.
Je cherche avec mes copains
L’organisation peut varier : en groupe ou en binômes, mais c’est toujours un problèmes à faire à plusieurs. Si un élève à une question, c'est dans le groupe qu'il doit essayer de trouver la réponse; c'est un travail collaboratif. Les attendus, les conseils et la correction de cet exercice de recherche sont à chaque fois précisés.
Le petit détective
Contrairement à l’exercice Je cherche avec mes copains, cet exercice de recherche est à mener individuellement. Ici, l’enseignant devra surtout tenir compte des procédures mises en oeuvre et des recherches effectuées par l’élève. Lors de la correction, il sera intéressant d'inviter un élève à expliquer oralement la démarche qu'il a suivie.
À la maison
 Chaque leçon se termine par un prolongement à faire hors de la classe, en famille par exemple.
Chaque leçon se termine par un prolongement à faire hors de la classe, en famille par exemple.
Je fais le point
Chaque période se conclut, dans les Cahiers, par une séance Je fais le point. C’est l’occasion pour les élèves de se préparer à l’évaluation. Des fiches Je fais l’évaluation, conçues dans le même esprit, avec des exercices très proches mais comportant d’autres variables didactiques, sont téléchargeables sur le site Ressources. Elles sont accompagnées d’une grille des compétences à compléter. ➥ maths-leonie.editions-bordas.fr
Les outils de la méthode
Les supports d'apprentissage pour l'élève
Les Cahiers - 13,50 €
Les deux Cahiers sont vendus ensemble.
Le Cahier 1 correspond aux périodes 1 et 2.
Le Cahier 2 correspond aux périodes 3, 4 et 5.
Commander
au forfait enseignant Feuilleter
Le livret de jeux - 4,99 €
Le jeu fait partie intégrante de la méthode Les Maths avec Léonie car il
favorise la mémorisation et suscite l’implication personnelle de l’élève.
Il permet également d’appréhender différemment la notion étudiée et
de lever d’éventuels blocages, sans crispation.
Chaque leçon propose un jeu en lien avec la compétence travaillée qui permet
à l’élève de s’entraîner en manipulant. Les règles du jeu sont décrites
et illustrées dans le Livret de jeux. Elles sont également téléchargeables
sur le site Ressources.
Ces activités reposent sur des jeux de cartes, des cubes,
des jetons, des formes géométriques souvent déjà
présentes dans les classes. La plupart de ces ressources
peuvent être téléchargées gratuitement sur le site Ressources.
Commander
le livret de jeux Feuilleter
le livret de jeux
La manipulation
La manipulation tient une place primordiale dans l’enseignement des mathématiques
car elle suscite la réflexion et permet de construire
durablement les connaissances. Elle permet un accès plus rapide à la représentation mentale des différents concepts abordés en mathématiques.
Elle est indispensable et constitue l’un des points
forts de la méthode Les Maths avec Léonie.
L’approche proposée par Les Maths avec Léonie repose en
partie sur les théories de Piaget, Bruner et Vygotski testées
et perfectionnées au cours des 30 dernières années.
Elle est fondée sur un enseignement explicite et sur des
étapes d’apprentissage bien identifiées et bien équilibrées :
1. L’étape concrète ou la manipulation qui permet à l’élève
d’approcher les notions de façon concrète et de se les approprier
avec son cheminement et ses mots. En échangeant
avec ses pairs, il verbalise son action.
2. L’étape imagée ou l’observation qui permet à l’élève de
passer de la manipulation à une représentation imagée.
Aidé de l’enseignant, il transforme ainsi son action en image
mentale.
3. L’étape abstraite ou la modélisation mathématique qui
permet à l’élève de transformer l’image mentale qu’il s’est
construite auparavant en une représentation abstraite. Lors
de cette phase, l’enseignant formalise progressivement la
notion. C’est seulement après cette étape qu’intervient la
trace écrite.
Pour aider les élèves dans ces passages du concret à l’image,
puis de l’image au concept, les enseignants pourront s’appuyer
sur ce Guide pédagogique qui propose des solutions
pour faire le lien entre ces étapes pour chacune des leçons.
Il précise également le matériel utilisé pour chaque leçon.
Ce matériel est très simple (cubes, barres, jetons, monnaie,
formes géométriques, horloges) et souvent déjà présent
dans les classes.
Le matériel à prévoir pour le CM1 (pour une classe de 25 élèves)
- Matériel de numération (cubes unités, barres de 10, plaques de 100, cubes mille : environ 250 de chaque catégorie)
- Jetons de couleurs différentes
- Dés
- Monnaie
- Balances Roberval et masses marquées
- Balances digitales
- Horloges individuelles
- Outils de géométrie (règle, équerre, compas)
- Papier calque ; papier pointé
- Formes géométriques planes
- Tangram
- Solides
- Petits cubes et bâtonnets en bois
- Trombones
- Calendriers
- Mètres ruban
- Géoplans et élastiques
- Géomiroirs
- Verres doseurs
Ressources téléchargeables gratuitement sur le site Ressources
- Cartes unités, dizaines, centaines, milliers
- Cartes fractions
- Cartes nombres entiers et décimaux
- Cartes durées
- Bandelettes de papier
- Grilles et quadrillages
- Grilles fractions décimales
- Cartes additions, soustractions, multiplications, divisions Énoncés de problèmes
- Cartes calculs
- Tableaux et graphiques
- Cartes et plans pour les déplacements
- Réseaux de points
- Droites graduées
- Bandes et carrés fractionnés à colorier
- Figures de géométrie
- Cartes constructions géométriques
- Plateaux de jeux et cartes à jouer
- Glisse-nombre
- Fiches solutions des jeux
Les outils pour l'enseignant
Le Fichier de différenciation - 39 €
Le Fichier de différenciation photocopiable propose des fiches
détachables pour faciliter la photocopie pour la classe. Ces fiches
s’adressent aussi bien aux élèves en difficulté avec la notion étudiée,
qu’à ceux qui ont besoin d’aller plus loin pour satisfaire leur soif
d’apprentissage.
Une fiche de remédiation est proposée pour chaque leçon.
Si besoin, l’enseignant pourra reprendre l’étape de manipulation
avec les élèves en difficulté avant de leur proposer ces fiches. Une
fiche d’approfondissement est également prévue pour chaque
leçon.
Commander
Le Guide pédagogique - 29€
Le Guide pédagogique est également téléchargeable gratuitement
sur le site Ressources.
Il contient : la présentation des outils de la méthode Les Maths
avec Léonie ; la présentation pédagogique de la méthode Les
Maths avec Léonie ; les conseils pédagogiques pour chaque leçon
et tous les corrigés des exercices des deux cahiers.
Les fiches d'entraînement en autonomie -Gratuit sur le site Ressources
Pour chaque leçon, une fiche d’entraînement en autonomie
est disponible gratuitement sur le site Ressources de la collection
maths-leonie.editions bordas.fr. Elle comporte des exercices
similaires à ceux présents dans le cahier. Seules les variables
didactiques changent de façon à pouvoir donner ces fiches aux
élèves en totale autonomie et à les placer en situation de réussite.
Les outils numériques
Les Cahiers numériques Gratuits pour
toute adoption
La version numérique dédiée aux enseignants est offerte pour toute adoption des Cahiers Les Maths avec Léonie CM1 pour la classe.
Les Cahiers en version numérique sont optimisés
pour la vidéoprojection ou l’usage sur
TNI. Ils offrent un affichage de qualité en
pleine page et permettent de zoomer sur les
parties des pages.
Le Guide pédagogique est inclus à la fin des
Cahiers en version numérique.
le numérique Télécharger
Le site Ressources
De nombreuses ressources gratuites sont disponibles sur le site de la collection.
Les documents PDF suivants peuvent être consultés en ligne et téléchargés pour être imprimés :
- Des Fiches d’entraînement en autonomie pour chaque leçon
- Le Guide pédagogique complet
- Les règles et les supports des jeux
- Des évaluations pour chaque période et leur grille de compétences
- Les traces écrites des J’apprends de chaque leçon
Vous ne faites pas encore parti de notre groupe Facebook ? On vous attend !
Nous avons créé ce groupe pour que vous puissiez partager votre expérience de la méthode Les Maths avec Léonie et vos astuces, échanger avec vos collègues et questionner nos auteurs. Vos avis sont essentiels pour que nous puissions vous proposer une offre éditoriale qui corresponde vraiment à vos besoins.











